Complexité
Classes de complexité
| Déterministe | Non-déterministe | |
|---|---|---|
| temps | P, EXPTIME | NP, NEXPTIME |
| espace | LOGSPACE, PSPACE, EXPSPACE | NLOGSPACE |
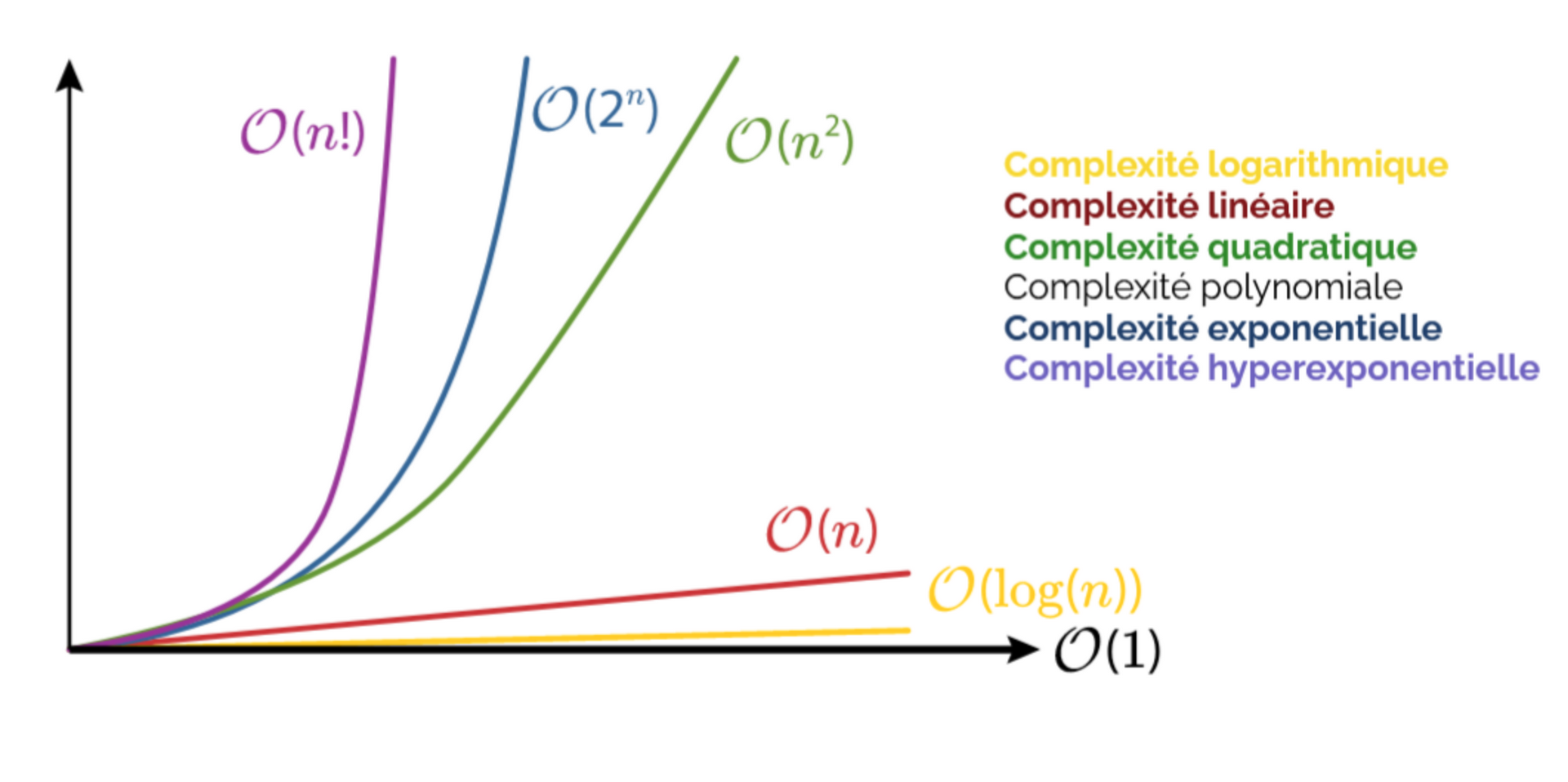
Complexité algorithmique
- O(1) : constant
- O(n) : linéaire
- O(log n) : logarithmique
- O(n log n) : quasi-linéaire
- O(n²) : quadratique
- O(n³) : cubique
- O(nᵏ) : polynomial
- O(2ⁿ) : exponentielle
- O(n!) : factorielle
| Algorithme | ||
|---|---|---|
| constant | O(1) | set |
| logarithmique | O(log n) | liste |
| linéaire | O(n) | recherche dichotomique, dans un tableau trié |
| quasi-linéaire | O(n log n) | tri d’un tableau (fusion) |
| quadratique | O(n²) | tri d’un tableau (insertion) |
| cubique | O(n³) | multiplication de matrices |
| polynomial | O(nᵏ) | |
| exponentielle | O(2ⁿ) | problème du sac à dos |
| factorielle | O(n!) | problème du voyageur de commerce |
Problèmes complexes
Problème du voyageur de commerce
- Problème NP-complet
- O(n!)
- 10 villes : 3 628 800
Problème du sac à dos
- Knapsack problem
- Problème NP-complet
- O(2ⁿ)
- 20 objets : 1 048 576
Problème du plus court chemin
- Aussi appelé longest common subsequence
- Problème NP-complet
- O(n²)
- 100 villes : 10 000
Stable marriage problem
- Aussi appelé problème des mariages stables (stable matching problem) ou problème des épouses de Gale et Shapley (Gale–Shapley algorithm)
- Problème NP-complet
- O(n²)
- 100 personnes : 10 000
- Algo 1 : Gale–Shapley (O(n²))
Vertex cover
- Aussi appelé couverture par sommets
- Algo 1 : brute force (O(2ⁿ))
- Algo 2 : approximation (O(n))
- Algo 3 : heuristique du degré (O(n²))
Clique
- Algo 1 : brute force (O(2ⁿ))
- Algo 2 : approximation (O(n))
Independent set
- Algo 1 : brute force (O(2ⁿ))
- Algo 2 : approximation (O(n))
Modularité
- Algo 1 : brute force (O(2ⁿ))
- Algo 2 : approximation (O(n))
Distance de Manhattan
- Algo 1 : brute force (O(n²))
Heuristique
- 2-approximation
- Degree
| Problème d’optimisation | Problème de décision |
|---|---|
| meilleure solution | oui/non |
| NP-complet | NP-difficile |